多元统计分析及软件应用

典型实验项目一：运输问题

对某种物资，设有m个产地A1, A2, …, Am，称它们为发点，其对应产量为a1, a2, …, am，称它们为产量；另有n个销地B1, B2, …, Bn，称它们为收点，其对应销量为b1, b2, …, bn，称它们为销量。又知，从产地（发点）Ai运至销地（收点）Bj，该种物资每单位的运价为ci j（ci j≥0）。试问：应如何安排调运方案，在满足一定要求的前提下，使总运费最低？

（1）实验内容

（2）实验过程

编写程序，完成这个运输问题。

! 3 Warehouse, 4 Customer Transportation Problem;

sets:

Warehouse /1..3/: a;

Customer /1..4/: b;

Routes( Warehouse, Customer) : c, x;

endsets

! Here are the parameters;

data:

a = 7, 4, 9;

b = 3, 6, 5, 6;

c = 3, 11, 3, 10,

1, 9, 2, 8,

7, 4, 10, 5;

enddata

! The objective;

[OBJ] min = @sum( Routes: c * x);

! The supply constraints;

@for( Warehouse(i): [SUP]

@sum( Customer(j): x(i,j)) <= a(i));

! The demand constraints;

@for( Customer(j): [DEM]

@sum( Warehouse(i): x(i,j)) = b(j));

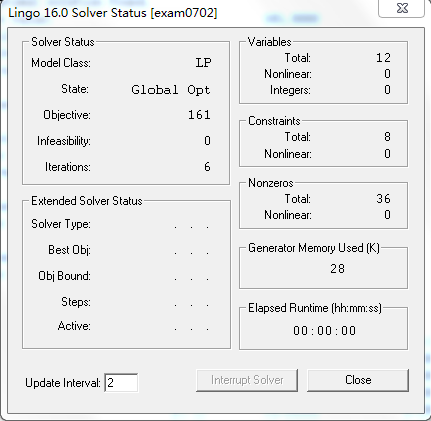
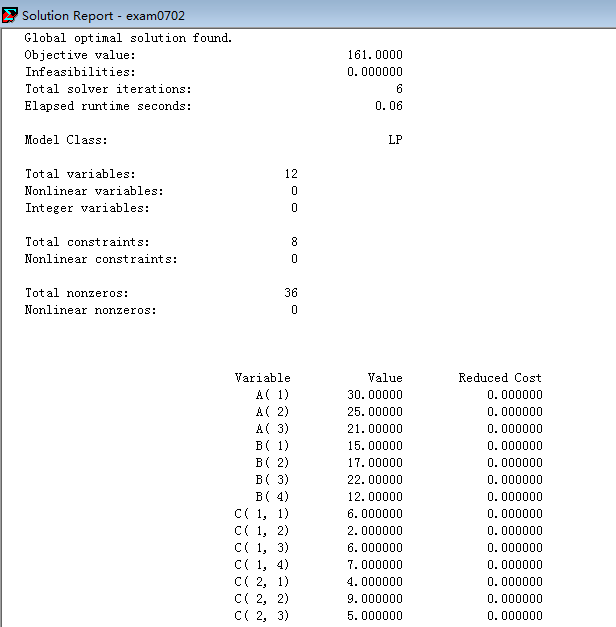
（3）实验功能与效果

本实验依托lingo软件，解决物流管理中的运输问题，培养学生分析运输问题的建模能力和利用软件求解问题的计算能力。